The Ultimate Guide To Spanning Tree Protocol

08 Jun 2024
Barokah1
Muskala

How does spanning help us understand complex systems? Spanning is the act of extending or reaching across something.

In mathematics, spanning refers to the concept of a set of vectors that spans a vector space. This means that any vector in the vector space can be expressed as a linear combination of the vectors in the spanning set. For example, in a three-dimensional space, the three vectors (1, 0, 0), (0, 1, 0), and (0, 0, 1) span the entire space, meaning that any three-dimensional vector can be expressed as a combination of these three vectors.

The concept of spanning has important applications in many fields, such as computer graphics, where it is used to create realistic images by spanning a set of polygons to form a three-dimensional object. Spanning is also used in network theory to design efficient communication networks, and in economics to model complex economic systems.

The ability to span complex systems is essential for understanding how they work and for developing effective ways to control them. Spanning provides a powerful tool for representing and analyzing complex systems, and it has applications in a wide range of disciplines.

Spanning

Spanning refers to the act of extending or reaching across something. It is a crucial concept in various fields, encompassing mathematics, computer graphics, network theory, and economics. Here are six key aspects of spanning:

Linear combination: Spanning vectors can be combined to form any vector in a vector space.
Vector space: A set of spanning vectors defines the dimensions of a vector space.
Geometric interpretation: Spanning vectors can be visualized as edges of a polygon or polyhedron.
Network connectivity: Spanning trees ensure that all nodes in a network are connected.
Economic modeling: Spanning models represent complex economic systems and their interactions.
Data representation: Spanning algorithms can be used to reduce the dimensionality of data.

These aspects highlight the diverse applications of spanning in different domains. By understanding these key concepts, we can effectively utilize spanning techniques to solve complex problems, model real-world systems, and gain deeper insights into various phenomena.

Linear Combination

Linear combination is a fundamental concept in the mathematical study of vector spaces. It refers to the ability to express any vector in a vector space as a combination of a set of linearly independent vectors called spanning vectors. The significance of linear combination lies in its role as a cornerstone of spanning, which is the process of extending or reaching across a mathematical space.

In the context of spanning, linear combination provides a powerful tool for representing complex vectors and geometric objects. Spanning vectors act as the building blocks that can be combined to form any vector within the vector space. This concept finds practical applications in various fields, including computer graphics, where it is used to construct three-dimensional models, and in network theory, where it helps design efficient communication systems.

To illustrate the importance of linear combination in spanning, consider a three-dimensional vector space. Any vector in this space can be expressed as a linear combination of three linearly independent vectors, often represented as the unit vectors (1, 0, 0), (0, 1, 0), and (0, 0, 1). This means that any three-dimensional vector can be uniquely represented by a combination of these three spanning vectors.

The concept of linear combination and spanning is essential for understanding vector spaces and their applications in various scientific and engineering disciplines. It provides a framework for representing and manipulating complex vectors and geometric objects, making it a valuable tool for problem-solving and analysis.

Vector space

In mathematics, a vector space is a collection of vectors that can be added together and multiplied by scalars. The dimensions of a vector space are determined by the number of linearly independent vectors that span the space. These spanning vectors form a basis for the vector space, and any vector in the space can be expressed as a linear combination of the basis vectors.

Linear independence: The spanning vectors of a vector space must be linearly independent. This means that none of the vectors can be expressed as a linear combination of the other vectors.
Basis: The set of spanning vectors that form a basis for a vector space is unique. This means that any other set of spanning vectors for the same vector space must have the same number of vectors.
Dimension: The dimension of a vector space is equal to the number of vectors in a basis for the space. This means that all vector spaces with the same dimension have the same number of spanning vectors.

The concept of spanning vectors and vector spaces is essential for understanding linear algebra and its applications. Spanning vectors provide a way to represent and manipulate vectors in a geometric way, and they are used in a wide variety of applications, including computer graphics, physics, and engineering.

Geometric interpretation

In mathematics, a polygon is a two-dimensional shape with straight sides. A polyhedron is a three-dimensional shape with flat faces. Both polygons and polyhedrons can be constructed by connecting a set of points with line segments. The line segments that connect the points are called edges.

In the context of spanning, the edges of a polygon or polyhedron can be visualized as spanning vectors. Spanning vectors are vectors that span a vector space. This means that any vector in the vector space can be expressed as a linear combination of the spanning vectors. In other words, the spanning vectors form a basis for the vector space.

The geometric interpretation of spanning vectors is important because it provides a way to visualize the concept of spanning. By visualizing the spanning vectors as edges of a polygon or polyhedron, we can better understand how they span the vector space. This understanding is essential for using spanning vectors to solve problems in a variety of fields, including computer graphics, physics, and engineering.

For example, in computer graphics, spanning vectors are used to create three-dimensional models. By understanding how spanning vectors can be visualized as edges of a polygon or polyhedron, computer graphics artists can create more realistic and complex models.

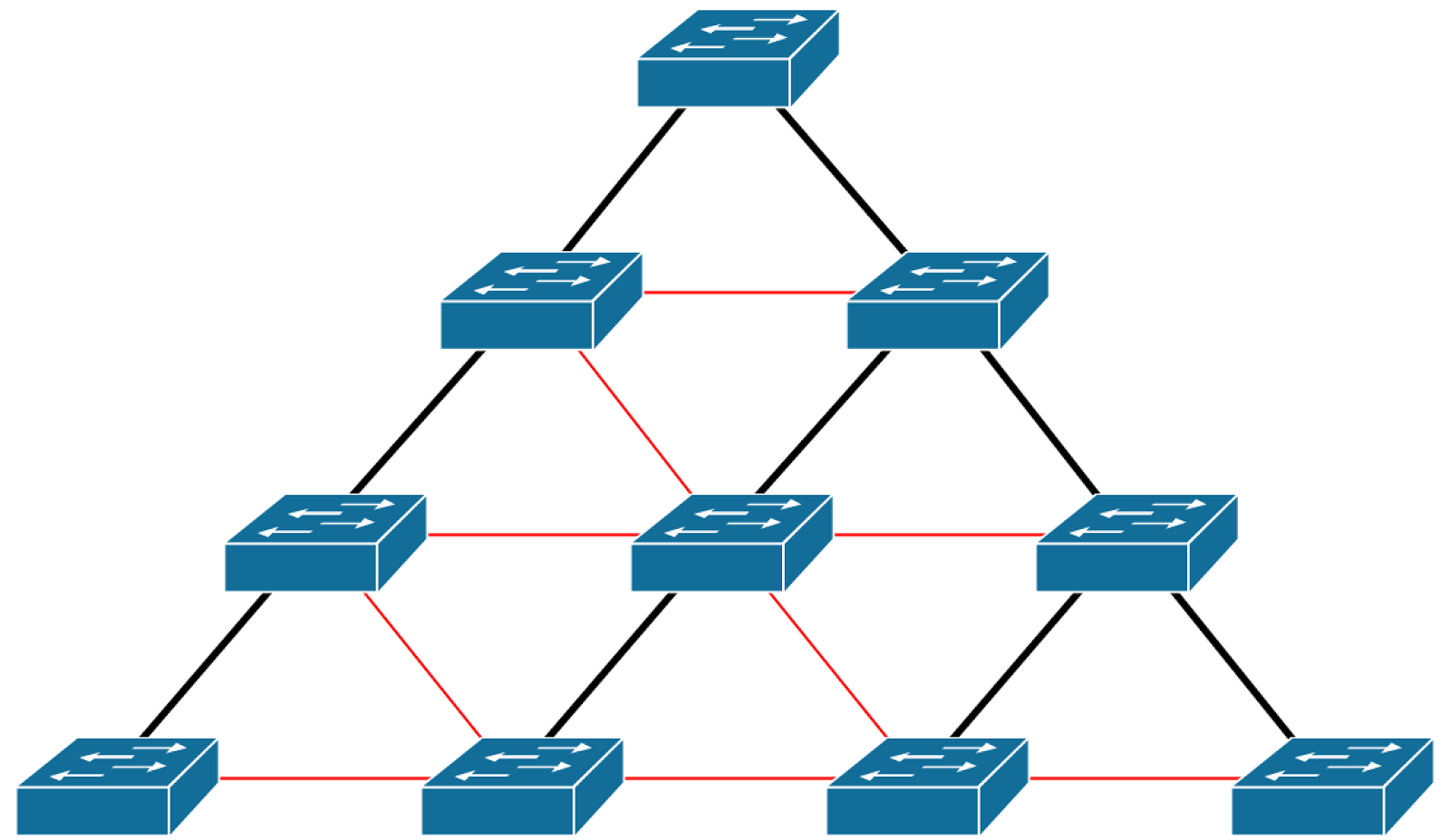
Network connectivity

In the realm of computer networks, spanning trees play a crucial role in maintaining network connectivity. A spanning tree is a subgraph of a network that connects all the nodes without creating any loops. This ensures that all nodes can communicate with each other, even if some of the links in the network fail.

Ensuring reliability: Spanning trees provide a backup path for data transmission in case one of the links in the network fails. This redundancy enhances the reliability of the network and ensures that critical data and applications remain accessible.
Optimizing network performance: By eliminating loops, spanning trees prevent network congestion and improve overall network performance. This is particularly important in large and complex networks where multiple paths may exist between nodes.
Facilitating network management: Spanning trees simplify network management by providing a clear and concise view of the network topology. This makes it easier for network administrators to identify and troubleshoot any connectivity issues.
Applications in various network protocols: Spanning trees are used in various network protocols, including the Spanning Tree Protocol (STP) and the Rapid Spanning Tree Protocol (RSTP). These protocols ensure that only one spanning tree is active at a time, preventing network loops and maintaining network stability.

In summary, spanning trees are essential for ensuring network connectivity, reliability, and performance. They provide a structured and efficient way to connect all nodes in a network, even in the presence of network failures or complex topologies.

Economic modeling

In economics, spanning models play a vital role in representing and analyzing complex economic systems. These models utilize spanning trees to capture the interconnectedness and dependencies among various economic agents, sectors, and markets.

The significance of spanning models lies in their ability to simulate the behavior of economic systems under different scenarios and policy interventions. By incorporating factors such as production, consumption, and trade, these models can provide valuable insights into economic dynamics, market equilibria, and the impact of shocks or changes in economic conditions.

One practical application of spanning models is in the analysis of supply chains. By constructing spanning trees that represent the network of suppliers, manufacturers, and distributors, economists can assess the resilience and efficiency of the supply chain. This helps identify potential bottlenecks, optimize inventory levels, and devise strategies to mitigate disruptions.

Moreover, spanning models have been employed to study financial markets. By modeling the interconnectedness of banks and other financial institutions, these models can assess systemic risk and identify potential vulnerabilities in the financial system. This understanding aids policymakers in developing regulations and policies to enhance financial stability.

In summary, spanning models are powerful tools for economic analysis and policymaking. Their ability to represent complex economic systems and interactions enables researchers and policymakers to gain deeper insights into economic behavior, simulate different scenarios, and devise informed decisions.

Data Representation

In the realm of data analysis, spanning algorithms play a pivotal role in reducing the dimensionality of data. Dimensionality reduction is a technique used to transform high-dimensional data into a lower-dimensional space while preserving essential information. Spanning algorithms achieve this by identifying the most significant features or components that capture the majority of the data's variance.

The significance of dimensionality reduction lies in its ability to enhance data visualization, improve computational efficiency, and facilitate machine learning algorithms. By reducing the number of features, spanning algorithms make data more manageable, allowing for easier interpretation and analysis. This is particularly beneficial in high-dimensional datasets, where traditional methods may struggle to extract meaningful insights.

One practical application of spanning algorithms is in image compression. Images can be represented as high-dimensional vectors, with each pixel contributing to the vector's dimensionality. Spanning algorithms can reduce the dimensionality of these vectors by identifying the most dominant features, such as edges and textures. This compressed representation allows for efficient storage and transmission of images without sacrificing visual quality.

Furthermore, spanning algorithms are used in natural language processing (NLP) to reduce the dimensionality of text data. By identifying the most important words and phrases, spanning algorithms create a lower-dimensional representation of the text that retains its semantic meaning. This reduced representation can then be used for tasks such as text classification and topic modeling.

In summary, spanning algorithms play a crucial role in data representation by reducing the dimensionality of data. This reduction enhances data visualization, improves computational efficiency, and facilitates machine learning algorithms. The practical applications of spanning algorithms are vast, ranging from image compression to natural language processing.

Frequently Asked Questions about Spanning

This section addresses frequently asked questions and misconceptions concerning the concept of spanning.

Question 1: What is the primary purpose of spanning in mathematics?

Spanning is a fundamental mathematical concept that involves extending or reaching across a space. It plays a vital role in defining vector spaces and their dimensions. Spanning vectors form the basis for representing any vector within that space, enabling efficient analysis and problem-solving.

Question 2: How does spanning contribute to network connectivity?

In network theory, spanning trees are crucial for ensuring connectivity and data transmission. By creating a connected subgraph without loops, spanning trees guarantee that all nodes can communicate, even in the event of link failures. This enhances network reliability and efficiency.

Question 3: What is the significance of spanning models in economics?

Spanning models are powerful tools in economics for representing complex systems and their interactions. These models employ spanning trees to capture the interconnectedness of agents, sectors, and markets. By simulating economic dynamics and analyzing market equilibria, spanning models provide valuable insights for policymakers and researchers.

Question 4: How does spanning aid in data representation?

Spanning algorithms are employed in data analysis to reduce the dimensionality of high-dimensional data. By identifying the most significant features, spanning algorithms create lower-dimensional representations that preserve essential information. This enhances data visualization, improves computational efficiency, and facilitates machine learning algorithms.

Question 5: What are the practical applications of spanning?

Spanning has diverse practical applications across various fields. In computer graphics, it is used to create realistic 3D models. In network theory, it optimizes network connectivity and performance. Economic modeling leverages spanning to simulate complex systems and analyze market dynamics. Data analysis employs spanning algorithms for dimensionality reduction and improving machine learning efficiency.

Question 6: What are some common misconceptions about spanning?

A common misconception is that spanning is limited to mathematical applications. However, its principles and techniques find applications in a wide range of disciplines, including computer science, economics, and data analysis.

In summary, spanning is a versatile concept with applications across multiple domains. It extends beyond mathematical foundations to encompass practical problem-solving and analysis in various fields.

This concludes the frequently asked questions about spanning. For further exploration, refer to the additional sections in this article.

Conclusion

Our exploration of spanning has delved into its diverse applications, ranging from mathematics and computer science to economics and data analysis. Spanning empowers us to represent complex systems, ensure network connectivity, analyze economic dynamics, and reduce data dimensionality.

As we continue to navigate increasingly complex challenges, the concept of spanning will undoubtedly play an even more prominent role. Its ability to uncover hidden patterns, optimize resource allocation, and enhance prediction accuracy makes it an invaluable tool for researchers, analysts, and decision-makers alike.

The Essential Guide To A Sparkling Spring Cleanup: Revitalize Your Home
The Ultimate Guide To Uncover The Whereabouts Of Noah's Ark
Discover Exclusive Savings: Sign Up Now For Lowe's Military Discounts!