Descriptive Examples Of Associative And Commutative Properties

13 Jun 2024
Barokah1
Muskala

Looking for clear-cut examples to grasp the concepts of associative and commutative properties?

In mathematics, these properties define how specific operations can be grouped and rearranged without altering the result. Let's delve into some illustrative examples to solidify your understanding.

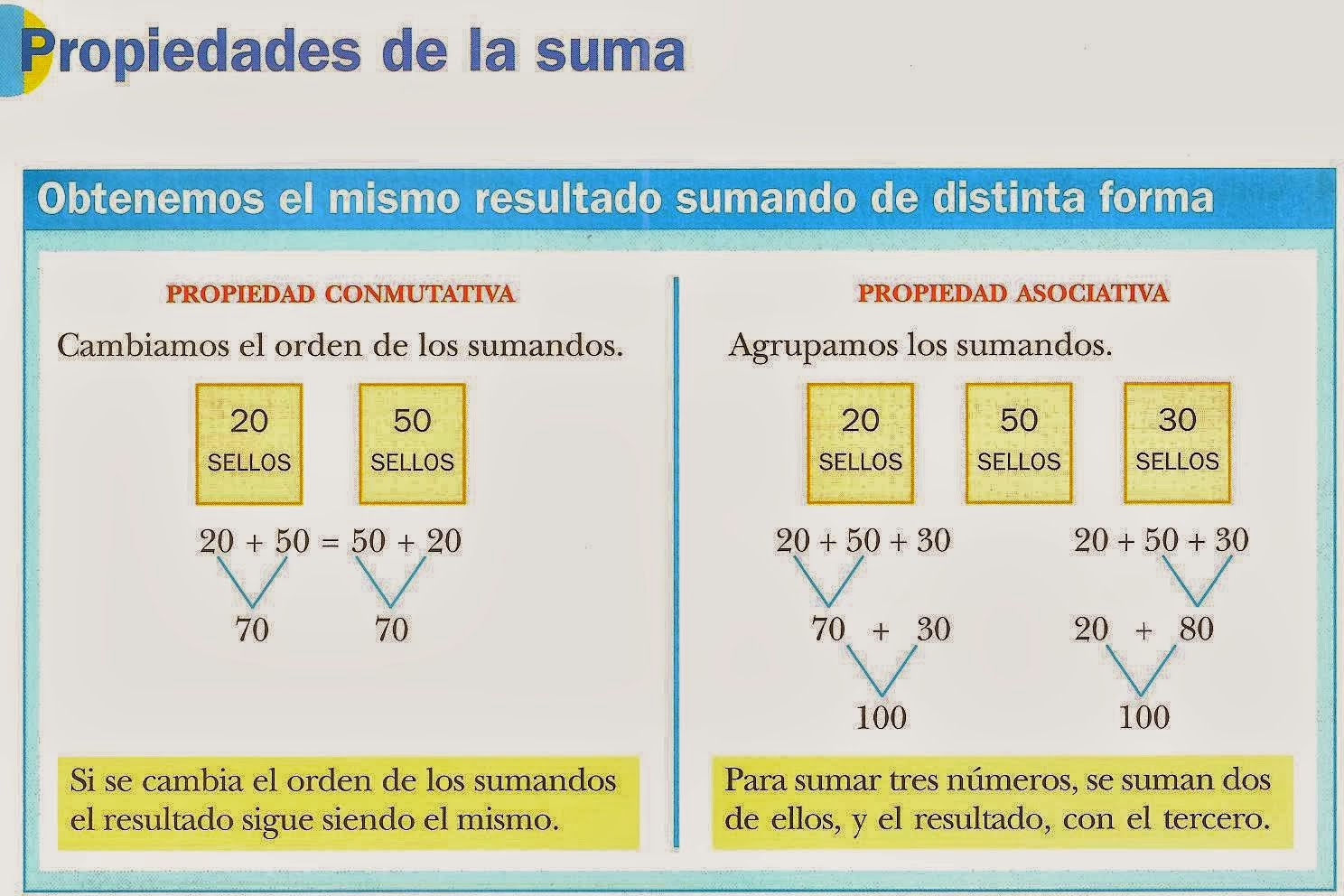
The associative property allows you to change the grouping of numbers when adding or multiplying without affecting the outcome. For instance, (2 + 3) + 4 equals 2 + (3 + 4), and (2 3) 4 equals 2 (3 4).

The commutative property, on the other hand, lets you change the order of numbers when adding or multiplying without altering the result. For example, 2 + 3 equals 3 + 2, and 2 3 equals 3 2.

These properties are essential building blocks in algebra and higher mathematics, ensuring that equations remain balanced and operations can be performed efficiently.

Examples of Associative and Commutative Properties

These properties are fundamental in mathematics, defining how operations can be grouped and rearranged without altering the result. Here are five key aspects to consider:

Grouping: Associative property allows for changes in grouping when adding or multiplying.
Order: Commutative property allows for changes in the order of numbers when adding or multiplying.
Algebra: These properties serve as building blocks in algebra and higher mathematics.
Equations: They ensure that equations remain balanced during operations.
Efficiency: They facilitate efficient operation performance.

These aspects are interconnected. For instance, the associative property enables efficient grouping of large sets of numbers, while the commutative property allows for flexible reordering of addends or factors. Together, they simplify complex mathematical expressions and enhance problem-solving capabilities.

Grouping

The associative property is a fundamental concept in mathematics that allows for the grouping and re-grouping of numbers in addition and multiplication without altering the final result. It states that the way in which numbers are grouped together does not affect the overall sum or product.

Real-life examples of the associative property in action include:

When calculating the total cost of groceries, you can group the items in any order and the total will remain the same. For instance, (apples + oranges) + bananas = apples + (oranges + bananas).
When multiplying a series of numbers, the order in which you group the factors does not affect the final product. For example, (2 3) 4 = 2 (3 4).

Understanding the associative property is crucial because it allows us to simplify complex mathematical expressions, solve equations more efficiently, and perform mental calculations with greater accuracy. It is a foundational concept that underpins much of modern mathematics and its applications.

Order

The commutative property is another fundamental concept in mathematics that deals with the order of numbers in addition and multiplication. It states that the order in which numbers are added or multiplied does not affect the final result.

Real-life examples of the commutative property in action include:

When calculating the total cost of groceries, the order in which you add up the prices of the items does not affect the total. For instance, apples + oranges = oranges + apples.
When multiplying a series of numbers, the order in which you multiply the factors does not affect the final product. For example, 2 3 = 3 2.

Understanding the commutative property is crucial because it allows us to simplify complex mathematical expressions, solve equations more efficiently, and perform mental calculations with greater accuracy. It is a foundational concept that underpins much of modern mathematics and its applications.

The commutative property is closely related to the associative property. Together, these two properties allow us to group and re-group numbers in addition and multiplication without altering the final result. This makes it easier to solve complex mathematical problems and to perform calculations mentally.

Algebra

The associative and commutative properties are essential building blocks in algebra and higher mathematics. They allow us to simplify complex mathematical expressions, solve equations more efficiently, and perform mental calculations with greater accuracy. These properties are so important because they provide a solid foundation for understanding more advanced mathematical concepts.

For example, the associative property allows us to group numbers in different ways when adding or multiplying without changing the result. This is a fundamental concept in algebra, where we often need to simplify complex expressions by grouping terms in different ways. The commutative property allows us to change the order of numbers when adding or multiplying without changing the result. This is also a fundamental concept in algebra, where we often need to rearrange terms in equations to solve them.

Without the associative and commutative properties, algebra would be much more difficult. These properties make it possible to simplify complex expressions, solve equations, and perform mental calculations with greater accuracy. They are essential building blocks for understanding more advanced mathematical concepts.

Equations

The associative and commutative properties play a crucial role in ensuring that equations remain balanced during operations. These properties allow us to group and rearrange numbers in addition and multiplication without changing the result. This is essential for solving equations, as it allows us to simplify complex expressions and isolate the variable on one side of the equation.

Simplification: The associative and commutative properties allow us to simplify complex expressions by grouping and rearranging terms. This makes it easier to solve equations, as we can reduce the number of terms and simplify the expression.
Isolation: The associative and commutative properties allow us to isolate the variable on one side of the equation. This is essential for solving equations, as it allows us to find the value of the variable.
Balancing: The associative and commutative properties ensure that equations remain balanced during operations. This means that the sum of the terms on one side of the equation is equal to the sum of the terms on the other side of the equation.

Without the associative and commutative properties, it would be much more difficult to solve equations. These properties provide a solid foundation for understanding algebra and higher mathematics.

Efficiency

The associative and commutative properties are essential for efficient operation performance in mathematics. They allow us to group and rearrange numbers in addition and multiplication without changing the result. This can save time and effort when performing complex calculations.

For example, consider the following calculation:

(2 + 3) + 4

Using the associative property, we can group the numbers in a different way:

2 + (3 + 4)

This gives us the same result, but it is easier to calculate because we can first add 3 and 4, and then add the result to 2.

The commutative property can also be used to improve efficiency. For example, consider the following calculation:

2 3 4

Using the commutative property, we can change the order of the factors:

2 4 3

This gives us the same result, but it may be easier to calculate because we can first multiply 2 and 4, and then multiply the result by 3.

The associative and commutative properties are essential for efficient operation performance in mathematics. They allow us to simplify complex calculations and save time and effort.

In conclusion, the associative and commutative properties are fundamental to mathematics. They provide a solid foundation for understanding algebra and higher mathematics, and they facilitate efficient operation performance. These properties are essential for solving complex mathematical problems and performing calculations with accuracy.

Frequently Asked Questions About Associative and Commutative Properties

This section aims to clarify common misconceptions and address frequently asked questions regarding the associative and commutative properties, providing a deeper understanding of these fundamental mathematical concepts.

Question 1: What is the associative property?

The associative property states that the grouping of numbers in addition or multiplication does not affect the result. For example, (2 + 3) + 4 is equal to 2 + (3 + 4).

Question 2: What is the commutative property?

The commutative property states that the order of numbers in addition or multiplication does not affect the result. For example, 2 + 3 is equal to 3 + 2.

Question 3: How are the associative and commutative properties related?

The associative and commutative properties are closely related. Together, they allow for flexibility in grouping and ordering numbers during mathematical operations without altering the outcome.

Question 4: Why are these properties important in mathematics?

These properties are crucial in mathematics as they simplify complex expressions, facilitate equation solving, and enable efficient operation performance.

Question 5: How can I apply these properties in real-life situations?

The associative and commutative properties find applications in various real-life scenarios, such as calculating expenses, distributing resources, or solving problems involving numerical data.

Question 6: Are there any limitations or exceptions to these properties?

The associative and commutative properties generally hold true for addition and multiplication operations involving real numbers. However, they may not apply to other mathematical operations or in specific mathematical contexts.

In summary, the associative and commutative properties are fundamental concepts that provide a solid foundation for mathematical operations. Understanding and applying these properties enhances problem-solving abilities and deepens the comprehension of mathematical principles.

Proceed to the next section for further exploration of these properties and their significance.

Conclusin

En el transcurso de este artculo, hemos explorado en profundidad los conceptos de las propiedades asociativa y conmutativa, examinando su importancia y proporcionando ejemplos ilustrativos. Estas propiedades fundamentales sientan las bases para las operaciones matemticas, simplifican expresiones complejas y permiten resolver ecuaciones con mayor eficacia.

Comprender y aplicar las propiedades asociativa y conmutativa no solo mejora las habilidades para resolver problemas, sino que tambin fortalece la comprensin general de los principios matemticos. Al aprovechar estas propiedades, podemos abordar clculos complejos con confianza y precisin.

All About Plus Size Measurements: A Comprehensive Guide
Common Examples Of Polar Covalent Bonds In Chemistry
Discover The Best Bargains For Quality Scrap Aluminium